https://www.acmicpc.net/problem/1072
# 학습 키워드
1. 이분탐색
특정 조건을 만족하는 값을 찾기 위해 탐색 범위를 반으로 줄여가는 방법을 사용했다. 이 문제에서는 승률이 변하는 최소 게임 수를 찾기 위해 이분탐색을 활용했다.
2. 수학적 연산과 반올림 문제
승률 계산 시 (100*y)//x와 같은 정수형 연산을 통해 승률을 구하고, 정수로 표현해 소수점 문제를 방지했다.
3. 예외처리
특정 조건을 만족할 수 없는 경우(승률이 99% 이상인 경우)에 대한 예외 처리가 필요했다.
# 문제 접근 방법
1. 문제 분석
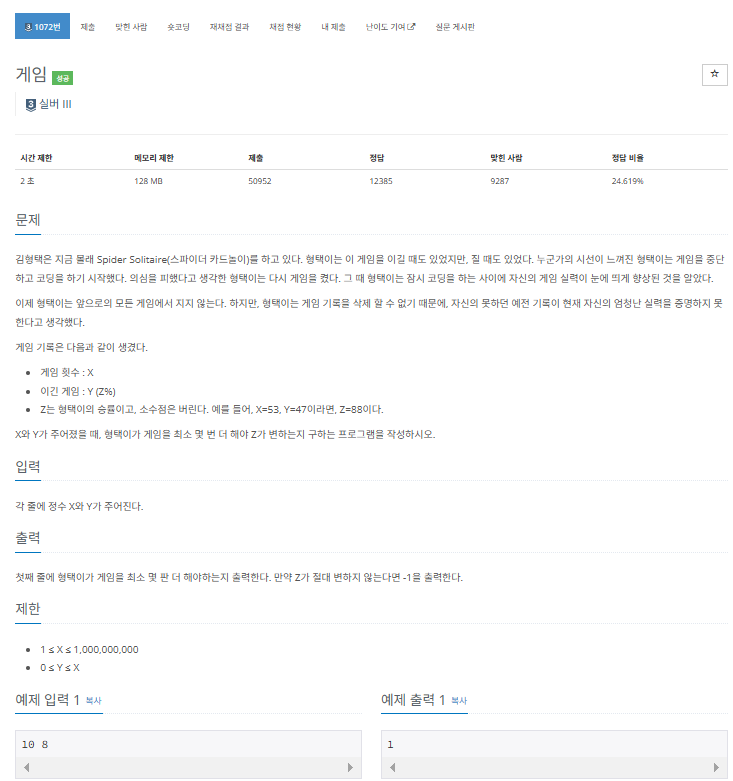
주어진 x(총 게임 수)와 y(이긴 게임 수)에서 승률 z를 구하고, 승률 z가 증가할 때 필요한 최소 게임 수를 구하는 문제이다.
- 승률 z가 99% 이상이면 게임 수를 늘려도 승률이 거의 변하지 않으므로, 이때는 -1을 출력한다.
2. 이분 탐색을 활용한 최소 게임 수 찾기
새로운 게임을 추가했을 때, 승률이 증가할 수 있는 최소의 게임 수를 찾기 위해 이분 탐색을 사용했다.
- left는 1, rigth는 x로 설정하고, 중간 값 mid를 이용하여 조건을 만족하는지 확인한다
- (y + mid) * 100 // (x + mid)를 통해 승률을 구하고, 기존 승률 z보다 크다면 mid값을 저장하고 rigth를 mid -1로 줄여 탐색 범위를 좁혀간다.
- 반대로 승률이 증가하지 않는 경우, left를 mid + 1로 증가시켜서 계속해서 탐색한다.
# 코드 작성
x,y = map(int,input().split())
z = (100*y)//x
if z >= 99:
print(-1)
else:
answer = 0
left = 1
right = x
while left <= right:
mid = (left+right)//2
if (y + mid) * 100 // (x + mid) <= z:
left = mid + 1
else:
answer = mid
right = mid - 1
print(answer)

# 회고
문제에서 승률 z가 99% 이상일 경우, 어떤 경우에도 승률을 올릴 수 없는 상태가 된다. 이와 같은 예외를 초기에 처리해줘야 불필요한 연산을 피할 수 있다. 문제풀이에서 초기 조건을 꼼꼼하게 확인하고 예외를 처리하는 것이 효율적임을 다시 느꼈다.
'대외활동 > 항해99' 카테고리의 다른 글
| 99클럽 코테 스터디 8일차 - 백준 2644번 촌수계산 [Python] (5) | 2024.11.04 |
|---|---|
| 99클럽 코테 스터디 5일차 TIL - 백준 2444번 알고리즘수업 너비우선탐색 1 [Python] (2) | 2024.11.01 |
| 99클럽 코테 스터디 4일차 TIL - 백준 24475번 알고리즘수업 깊이우선탐색1 [Python] (1) | 2024.10.31 |
| 99클럽 코테 스터디 3일차 TIL - 프로그래머스 입국심사 [Python] (1) | 2024.10.30 |
| 99클럽 코테 스터디 2일차 TIL - 백준 11561번 징검다리 [Python] (1) | 2024.10.29 |